- (If you find it hard to follow your arguments, then you can't expect the reader to be able to follow, right?)
We will restrict ourselves to facts about numbers for now.
Universal Statements
A universal statement (over a certain set a.k.a ‘‘universe of discourse’’  ) is a claim that for every number
) is a claim that for every number  in
in  , some fact (described by some predicate) holds over
, some fact (described by some predicate) holds over  . Mathematically, a universal statement is in the form
. Mathematically, a universal statement is in the form  .
.

Universal statements (over a set ) are proved as follows:
- Fix an arbitrary element
 .
. - Prove that
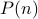 holds — usually by doing some algebra.
holds — usually by doing some algebra.
Let us now look at an example.
Example 1
Let's try to prove the following theorem.
Theorem. For every natural number  , the number
, the number 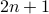 is an odd number.
is an odd number.
- Let
 be any fixed natural number.
be any fixed natural number. - Let
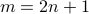 .
. - We are asked to show that
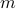 is odd.
is odd. - What does it mean for a natural number to be odd? By definition, that number has to leave a remainder of
 when divided by
when divided by 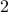 .
. - Let's see if
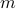 has a remainder
has a remainder  when divided by
when divided by 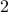 :
:
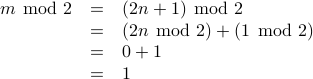 hspace mod 2 &=& (2 n + 1)hspace mod 2 &=& (2 nhspace mod 2) + (1hspace mod 2) &=& 0 + 1 &=& 1 end " />
hspace mod 2 &=& (2 n + 1)hspace mod 2 &=& (2 nhspace mod 2) + (1hspace mod 2) &=& 0 + 1 &=& 1 end " />
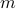
- We can conclude that is an odd number.
Let  be any fixed natural number. Let
be any fixed natural number. Let 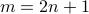 . Then
. Then
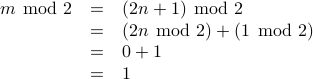 hspace mod 2 &=& (2 n + 1)hspace mod 2 &=& (2 nhspace mod 2) + (1hspace mod 2) &=& 0 + 1 &=& 1 end " />
hspace mod 2 &=& (2 n + 1)hspace mod 2 &=& (2 nhspace mod 2) + (1hspace mod 2) &=& 0 + 1 &=& 1 end " />
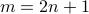
Hence is an odd number. QED.
Universal Statements With Implication
We now look at a special form of universal statements of the form:
Universal Statement With Implication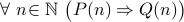 .
.
We recall that for given two propositions  and
and  (or predicates), the implication
(or predicates), the implication  is true if one of the following holds:
is true if one of the following holds:
- the premise
 and the conclusion
and the conclusion  are both true;
are both true; - the premise
 is false. (In this case it does not matter whether the conclusion holds true or not.)
is false. (In this case it does not matter whether the conclusion holds true or not.)
(An easy example is “If you win the bet, then I will give you $20.” If you don't win the bet, I can still give you $20 without breaking my promise!)
Following the general rule for universal statements, we write a proof as follows:
- Let
 be any fixed number in
be any fixed number in  .
. - There are two cases:
 does not hold, or
does not hold, or  holds.
holds. - In the case where
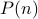 does not hold, the implication trivially holds.
does not hold, the implication trivially holds. - In the case where
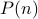 holds, we will now prove
holds, we will now prove 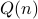 .
. - Typically, some algebra here to show that
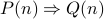 .
.
- Typically, some algebra here to show that
We can use a simple short-cut that avoids unnecessary language in such proofs.
- Let
 be any fixed number in
be any fixed number in 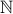 such that
such that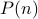 holds.
holds. - We will show that under these assumptions
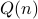 holds (typically by using some algebra).
holds (typically by using some algebra).
Example 2
Theorem. If  is an even number and
is an even number and 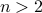 then
then  is composite.
is composite.
Here are our reasoning steps:
- Fix any natural number
 such that
such that  is even and
is even and 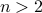 .
. - From this assumption, we can write
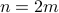 wherein
wherein 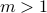 .
.  has two non-trivial factors
has two non-trivial factors 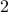 and
and 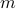 .
. is therefore composite. QED.
is therefore composite. QED.
Example 3
Theorem. For every natural number  , if
, if 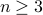 , then
, then 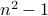 cannot be prime.
cannot be prime.
Here are the steps of our reasoning.
- Assume a given number
 such that
such that 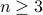 .
. - We will now show that
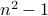 is a composite number.
is a composite number. - By elementary algebra, we see that
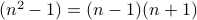 .
. - We note that
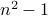 can be written as the product of two numbers.
can be written as the product of two numbers. - It remains to show that the factors of
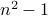 are not trivial. That is,
are not trivial. That is, 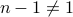 ( and therefore
( and therefore 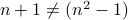 ).
). - Since
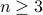 ,
,  . Therefore
. Therefore 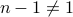 .
.
- Since
- We have just shown that
 and both
and both 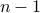 is greater than
is greater than  . Therefore
. Therefore 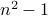 is composite. QED.
is composite. QED.
- By elementary algebra, we see that
Now we are going to learn two commonly used techniques: proof by cases and proof by contrapositive (for implication statements).
Proof by contrapositive
This technique is used for proving implications of the form 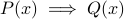 . Since an implication is always equivalent to its contrapositive, proving that
. Since an implication is always equivalent to its contrapositive, proving that 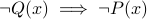 does the job.
does the job.
Example 4
Theorem. For any integer  , if
, if 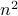 is even, then
is even, then  is even.
is even.
The statement in this theorem is equivalent to the contrapositive statement: For any integer  , if
, if  is not even, then
is not even, then 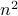 is not even. It suffices to prove this contrapositive statement here!
is not even. It suffices to prove this contrapositive statement here!
- Fix any odd integer
 .
. - By definition of odd integers,
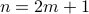 for some integer
for some integer 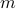 .
. - Then
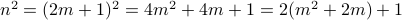 .
. - Hence
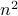 is an odd integer. QED.
is an odd integer. QED.
Caution: This technique is often useful but make sure you formulate the contrapositive statement properly before proving it!
Proof by cases
When given a statement to prove, sometimes it is easier to consider severl complementary scenarios, and prove the statement in each of the scenarios via different arguments.
Example 5
Prove that for any positive integers 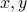 , if
, if 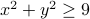 , then
, then 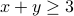 .
.
Since we are only concerned with positive integers  and the conclusion
and the conclusion 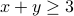 automatically holds when
automatically holds when  or
or 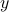 is greater than or equal to 3, we can consider the following cases:
is greater than or equal to 3, we can consider the following cases:
- Case 1:
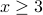 or
or 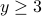 .
. - Case 2:
 , or equivalently,
, or equivalently, 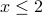 and
and 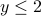 .
.
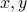
For any positive integers , we consider two different cases.
- Case 1:
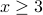 or
or 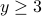 . Without loss of generality, suppose that
. Without loss of generality, suppose that 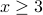 . Then the conclusion holds because
. Then the conclusion holds because  .
.
- Case 2:
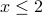 and
and 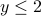 . We check if the premise
. We check if the premise 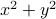 could ever hold in this case — there are only 3 cases to check because
could ever hold in this case — there are only 3 cases to check because 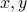 are positive integers!
are positive integers! - If
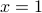 and
and  , then
, then  so the premise does not hold.
so the premise does not hold. - If
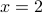 and
and  (or symmetrically
(or symmetrically 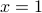 and
and 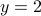 ), then
), then 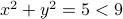 . So again the premise does not hold.
. So again the premise does not hold. - If
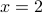 and
and 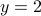 , then
, then  so the premise does not hold. Therefore in Case 2, the premise
so the premise does not hold. Therefore in Case 2, the premise 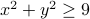 never holds. Then the implication
never holds. Then the implication 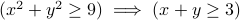 trivially holds in this case.
trivially holds in this case.
- If
In conclusion, the implication 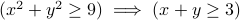 holds for all positive integers
holds for all positive integers 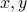 .
.
Universal statements involving ‘‘if and only iff’’
Finally, we look at the general proving techniques for one common type of universal statements:
Universal statements with implication and converse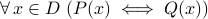
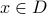
For proving such a statement, we usually proceed in two main steps after fixing any .
- Prove that
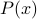 implies
implies 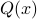 .
. - Prove that
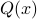 implies
implies 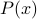 .
.
Example 6
Theorem. For any integer  ,
,  is even if and only if
is even if and only if 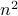 is even.
is even.